Our NSF Expeditions in Computing team aims to invent and demonstrate new experimental approaches to creating CIMs. While our team and others have performed a number of proof-of-principle demonstrations showing that CIMs can heuristically solve Ising problems, we have not yet experimentally shown a cost-effective system that can outperform state-of-the-art conventional methods running on state-of-the-art conventional processors. Two fundamental challenges we are tackling are: 1) how to build CIMs at large scale in a way that the underlying photonics processing is not bottlenecked by electronic processing, and 2) how to build CIMs that operate in a quantum regime that is intractable to simulate classically and delivers a computational advantage.
To address both challenges we are simultaneously working both on new experimental building blocks (at the device/component level) as well as new architectures (at the system level). Our device efforts are focused on miniaturization using nanophotonics. While all our implementations of programmable CIMs so far are based on discrete-component table-top optical systems, one important theme of this project is exploring paths towards on-chip realization of CIMs. Our team is designing and developing new nonlinear devices, such as optical parametric amplifiers, based on thin-film lithium niobate. In addition to reducing the footprint of CIMs and increasing the number of spins, miniaturized components also provide new or enhanced computing resources, which we are exploring both theoretically and experimentally. In the classical regime, miniaturization can lead to orders of magnitude improvements in energy consumption and speed. Nanophotonic devices also have the potential to allow us to explore modules in the quantum regime, and we are pursuing the generation and study of quantum states in nanophotonic CIMs, and their role in quantum-enhanced solution mechanisms in CIMs.
At the level of systems and architecture, we are exploring three different multiplexing strategies for constructing CIMs at large scale: time multiplexing, frequency multiplexing, and space multiplexing. All three involve tradeoffs between ease-of-construction, connectivity, and performance, and we aim to quantify these tradeoffs as well as mitigate the disadvantages of each strategy. Time-multiplexed CIMs, in which each spin is represented by a pulse of light in an optical cavity (typically a fiber loop), have been proven to scale to very large numbers of spins, but there is an open research challenge for how best to programmably couple spins without using electronic measurement-feedback, which limits the system performance. Frequency-multiplexed CIMs, in which each spin is represented by a frequency mode of an optical cavity, allows for very large numbers of spins and long-range coupling between spins, but with research challenges about mitigating the translational symmetry in the couplings, and achieving single-shot readout. Space-multiplexed CIMs, in which each spin is represented by a spatial optical mode, possibly as part of a cavity or possibly as part of a single-pass arrangement, offer a key computational benefit: the ability to construct matrix-vector multipliers where the scalar multiplications of each matrix element with an element of the spin vector all occur in parallel. Research challenges include scaling to large numbers (>1000) of spins and rapidly feeding the output of a matrix-vector multiplication through a nonlinearity and back as the input to the next multiplication. This work is primarily being pursuing with spatially parallel optical matrix-vector multipliers, but there is also an effort to implement a highly parallel electronic (field-programmable gate array) version, which could allow some of the advantages of the CIM strategy for solving Ising problems to be usable by the broader community before "conventional" (photonic) CIMs become broadly available.
___
### Experimental Thrusts
#### *Device/component Efforts*
Miniaturization: While all the implementations of programmable CIMs so far are based on discrete-component table-top optical systems, one important theme of this project is exploring paths towards on-chip realization of CIMs. These efforts range from design and development of the nonlinear building blocks (such as optical parametric amplifiers) to realization of a fully integrated programmable CIM towards large-scale machines. [Caltech/Stanford]
Quantum and classical resources: In addition to reducing the footprint of CIMs and increasing the number of spins, these studies also explore new or enhanced computing resources in nanophotonic CIMs compared to their table-top counterparts. In the classical regime, special attention is paid to energy and speed of CIMs, for which nanophotonic realization is expected to provide orders of magnitude advancement. In the quantum regime, the efforts range from realization of quantum states in nanophotonic CIMs to studying their dynamics and potential computing benefits. [Caltech/Stanford]
#### *Systems/architecture Efforts*
Development of time-multiplexed CIMs, in which each spin is represented by a pulse of light in an optical cavity (typically a fiber loop). This approach allows for very large numbers of spins to be represented, but with a research challenge of how to efficiently realize programmable coupling between spins. [Caltech/Stanford]
Development of frequency-multiplexed CIMs, in which each spin is represented by a frequency mode of an optical cavity. This approach also allows for very large numbers of spins and long-range coupling between spins, but with research challenges about mitigating the translational symmetry in the couplings, an unusual form a non-linearity across the spins, and achieving single-shot readout. [Cornell]
Development of space-multiplexed CIMs, in which each spin is represented by a spatial optical mode, possibly as part of a cavity or possibly as part of a single-pass arrangement. In space-multiplexed architectures, the key computational benefit is the ability to construct matrix-vector multipliers where the scalar multiplications of each matrix element with an element of the spin vector all occur in parallel. Research challenges including scaling to large numbers (>1000) of spins and rapidly feeding the output of a matrix-vector multiplication through a nonlinearity and back as the input to the next multiplication. This work is primarily being pursuing with spatially parallel optical matrix-vector multipliers, but there is also an effort to implement a highly parallel electronic (field-programmable gate array) version. [Cornell/USRA]
#### *Project*
Our CIM Expedition project is organized around four major themes: Fundamentals, Generalizations, Applications, and Benchmarking. While Fundamentals and Benchmarking focus mainly on developing broader and deeper understandings of current CIM prototypes, Generalizations and Applications explore CIM’s potential to advance both practical technology and new concepts in computer engineering. A snapshot of our research plan is provided by the graphic below.
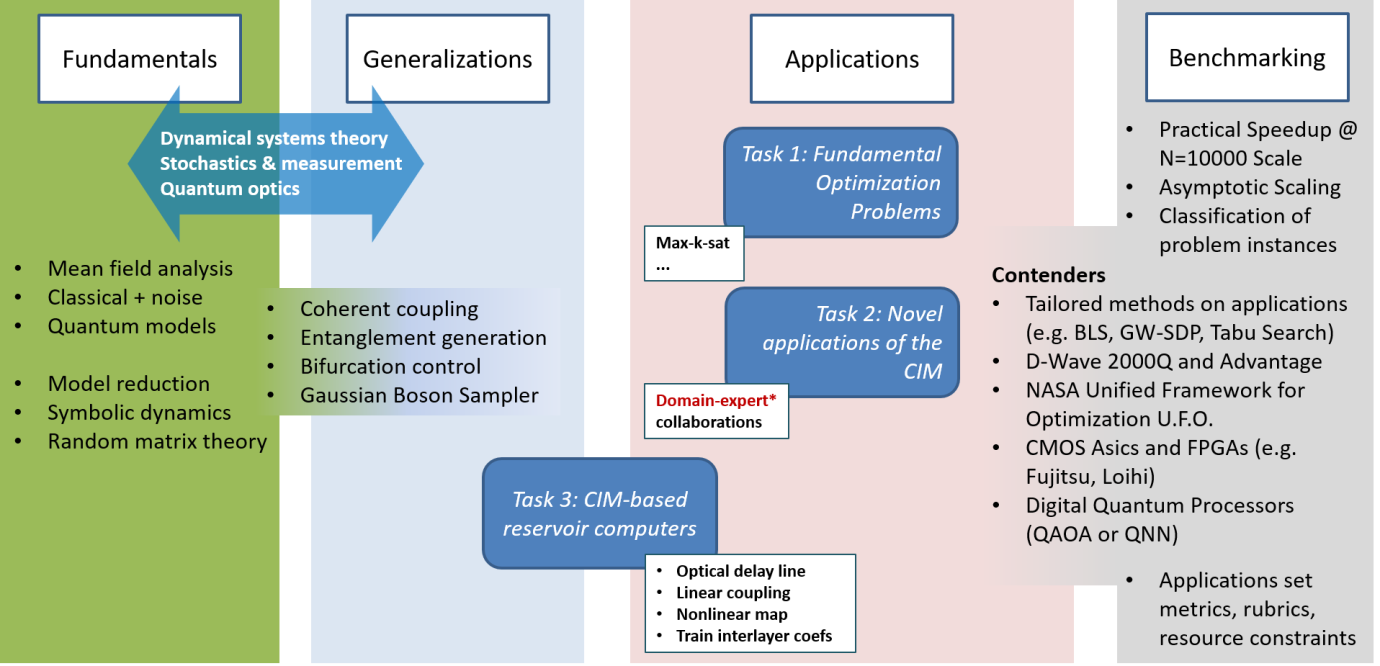
The theme of CIM Fundamentals encompasses detailed analysis of the physical operating principles of CIM hardware — what are the rate-limiting steps in optimization dynamics of current prototypes, how do they relate to the combinatorial structure of specific problem instances, and how do technical issues of noise and finite precision factor into computational performance? We plan to address such questions using an array of approaches based in quantum optics, dynamical systems theory, and random matrix theory.
The closely-related theme of CIM Generalizations draws upon these same core disciplines, but expands the research in the direction of manifestly quantum phenomena and potential improvements of the CIM architecture. If we work to further suppress decoherence in advance CIM prototypes can we sustain entanglement and observe non-classical interference effects that accelerate rate-limiting dynamics? Can we adapt ideas from multi-layer neural networks, message passing algorithms, and/or reservoir computing to improve upon the current approach for Ising-type optimizations? Can we broaden the class of problems for which CIM-type hardware is best suited?
In the CIM Applications theme we return to focus on capabilities of current CIM prototypes but will work to elaborate detailed and rigorous connections between specific needs of practical applications and CIM’s unique computational strengths and weaknesses. We will tackle issues such as efficient mapping from application-native to CIM-native problem formulations, as well as related issues regarding approximations and feasibility constraints. In this area we will work closely with application domain experts including collaborators in industry.
Our CIM Benchmarking activities will be led by our group at USRA/NASA, building on their extensive expertise in evaluating the performance of emerging quantum computing technologies and formulating fair comparisons against conventional digital computing approaches, considering both time-based metrics and auxiliary resource costs such as energy consumption. The results of this work will help us to draw a more complete and reliable picture of the trajectory of CIM prototype performance relative to other unconventional computing technologies. They will also enable us to analyze more thoroughly how classes of optimization problem instances map to different types of phase space topologies for the dynamic evolution of physical CIM hardware, which is critical for our fundamental understanding of CIM scaling.
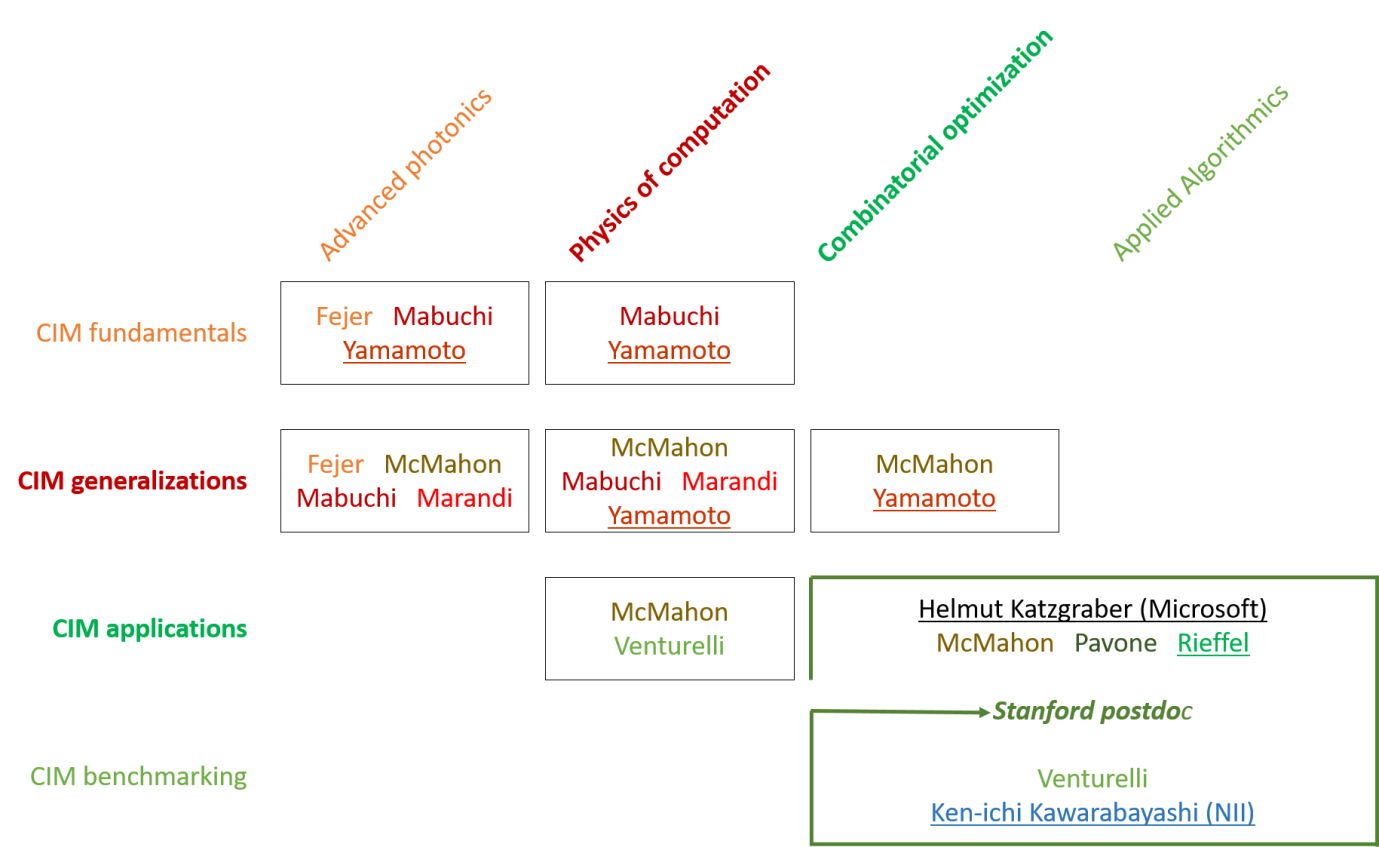
The above graphic illustrates the rough “org chart” of how our CIM Expedition’s constituent research groups map onto the four themes describe above, represented by rows of the table. The columns of the table indicate general domains of disciplinary expertise, highlighting the interdisciplinary nature of our effort spanning from device physics to core areas of computer science and applied mathematics